La cryptographie, c'est de la magie!
La cryptographie est LE pilier de la sécurité informatique. Elle repose sur des algorithmes qui vont transformer mathématiquement vos données afin d'en assurer l'authenticité (certitude sur l'identité de l'émetteur des données), l'intégrité (certitude que les données d'origine sont intègres), la confidentialité (certitude que personne d'autre que le destinataire ne pourra en prendre connaissance).
Les algorithmes.
Système numérique.
L'algorithme est une suite d'instructions ou d'opérations visant à résoudre un problème. Le problème dont il est question en cryptographie est lié à la factorisation de très grands nombres entiers (cryptographie asymétrique), des calculs sur des courbes elliptiques et des opérations de substitution permutation (cryptographie symétrique). Ces calculs sont réalisés avec les ordinateurs, qui fonctionnent avec des systèmes de numération utilisant la base 2, dans lesquels une donnée est décomposée dans la plus petite unité existante appelée un bit. Celui-ci ne peut prendre que 2 valeurs, soit 0, soit 1. Cette technologie est capable de calculer des clés cryptographiques donc de chiffrer. Elle ne permet par contre pas de faire le chemin en sens inverse (casser un chiffrement) dans un temps acceptable.
Système quantique.
Imaginez maintenant que la plus petite unité décomposant les données puisse prendre non pas 1 valeur parmi 2 mais 2 en même temps parmi une infinité, ça ouvre clairement de nouveaux horizons !
Ce fonctionnement correspond à la technologie quantique, dans laquelle la plus petite unité se nomme alors un bit quantique ou qubit. De plus, lorsque la technnologie numérique est contrainte d'effectuer des calculs séquentiels, la technologie quantique permet de les paralléliser. On perçoit alors intuitivement que les capacités de calcul s'en trouvent décuplées, on change d'univers. La conséquence est que les calculs nécessaires pour "casser" les algorithmes actuels qui reposent sur la factorisation de très grands nombres ou des logarithmes dicrets (cryptographie asymétrique) deviennent une réalité.
Certes, les ordinateurs basés sur cette technologie ne seront pas commercialisés demain, on estime même que le 1er ordinateur quantique ne sera pas commercialisé avant au moins 10 ans... Pourtant, Apple (dans iMessage), Signal, Tuta Mail ont déjà introduit des algorithmes post-quantiques dans leur chiffrement et tous les acteurs du secteur y travaillent.
Pourquoi ?
- D'abord parce que ce n'est pas parce qu'on annonce la commercialisation des premiers ordinateurs quantiques dans 10 ans qu'il n'y en aura pas en activité avant: l'histoire nous apprend que l'annonce du "cassage" d'un chiffrement est rarement publique (voir Enigma pendant la 2nde Guerre).
- Ensuite parce qu'une technique d'attaque nommée "récolter maintenant, déchiffrer plus tard" est déjà en place: son principe est de collecter aujourd'hui de la donnée chiffrée s'appuyant sur des clés cryptographiques de longue durée, pour la déchiffrer plus tard, lorsque la technologie nécessaire sera disponible.
Confidentialité des données : CHIFFREMENT.
Objectif : S'assurer que seul le destinataire d'un message pourra en prendre connaissance. Il est transformé de telle sorte que personne ne pourra le comprendre sans être en possession de la clé qui en ouvre l'accès.
Ce chiffrement peut être symétrique (une clé secrète partagée entre les utilisateurs permet de chiffrer et déchiffrer) ou asymétrique (une paire de clés publique/privée est utilisée pour chiffrer/déchiffrer).
Chiffrement symétrique (également nommé à clé secrète).
Principe.
L'émetteur utilise une clé secrète (qui est une suite de 128 ou 256 bits) pour transformer les données qu'il veut protéger en données chiffrées, puis il envoie le message chiffré au destinataire par le canal de son choix. Le destinataire reçoit le message chiffré puis il utilise la même clé secrète que l'expéditeur pour le déchiffrer et prendre ainsi connaissance du message originel.
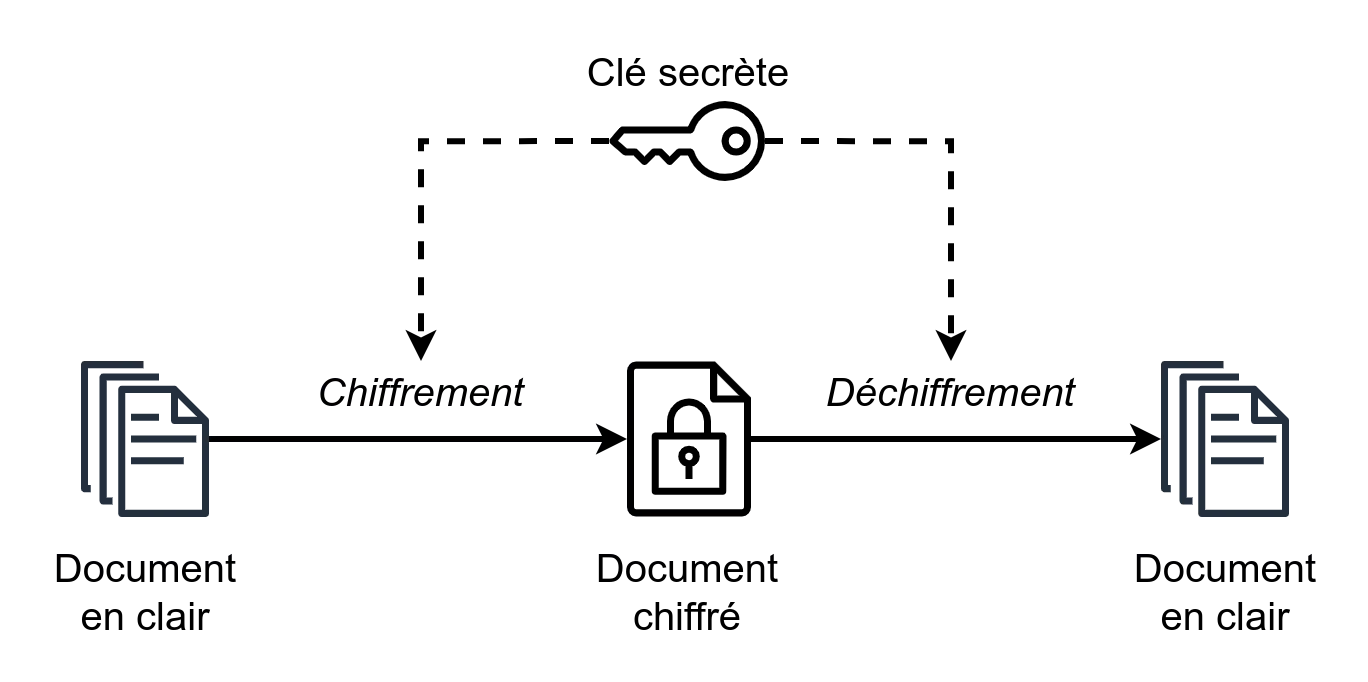
Par MarcT0K (icônes par JGraph) CC BY-SA 4.0
Exemple du résultat de chiffrement du mot "Bonjour"avec l'algorithme AES (Advanced Encryption Standard) et une clé aléatoire de 256 bits :
---------- texte chiffré ----------
9jua5EL34mZTva/NuNirTA==
------- fin du texte chiffré -------
L'inconvénient du chiffrement symétrique :
- il faut pouvoir échanger la clé secrète par un canal sécurisé.
- il y a autant de paires de clés à gérer qu'il y a d'utilisateurs.
Fonctionnement.
Les algorithmes chiffrent soient par blocs (AES, Serpent, Twofish) soit par flots aussi nommé par bits (ChaCha20), cette deuxième méthode étant plus rapide que la première dans le cadre d'une utilisation sans support matériel spécifique.
Dans le cas du chiffrement par blocs, la donnée est coupée en blocs de 128 bits puis chiffrés avec la clé (dont la taille est généralement comprise entre 128 et 256 bits).
La fonction utilisée par l'algorithme est itérée un certain nombre de fois (14 dans le cas d'AES-256): chaque itération (qu'on appelle tour) est le chiffrement du résultat précédent par une fonction mathématique appliquée avec une nouvelle clé mathématique.
C'est ce qui apporte de la robustesse au chiffrement (une attaque par clé apparentée sur AES-128 avec seulement 8 tours a été publiée en 2011).
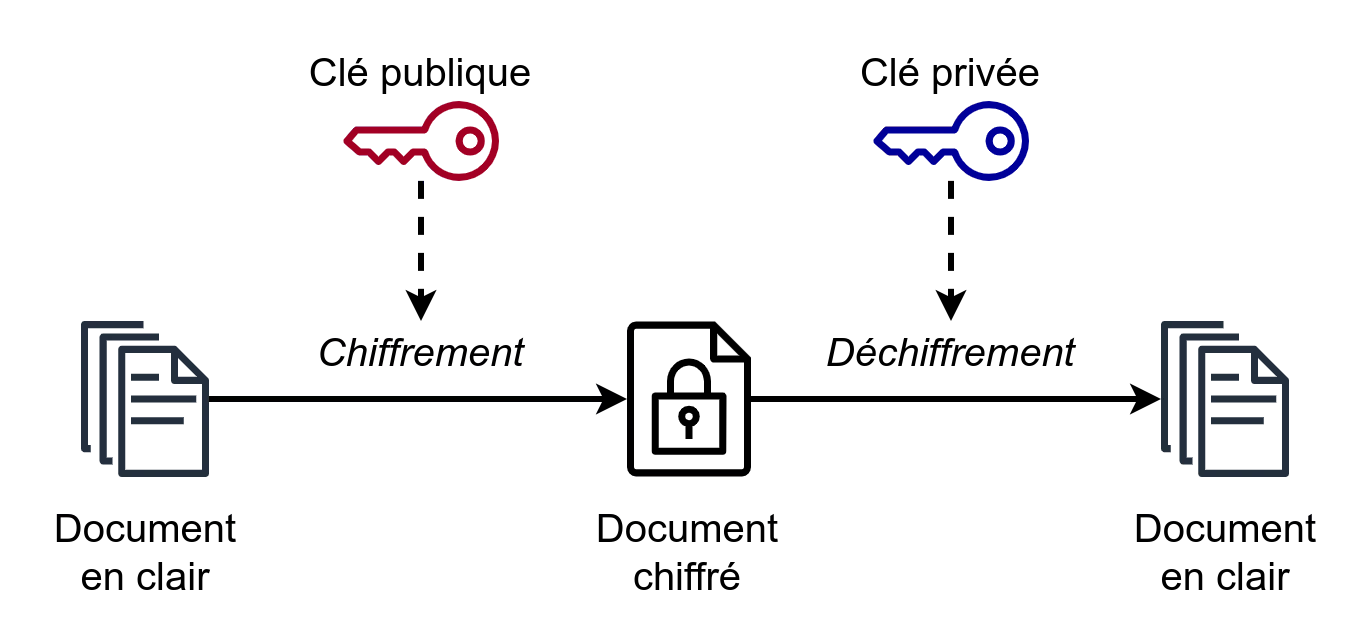
Chiffrement asymétrique (également nommé à clé publique).
Principe.
Un utilisateur génère un couple de clé et diffuse largement la clé publique (serveur de clés). Toute personne souhaitant lui envoyer un message pourra le faire en le chiffrant avec la clé publique de cet utilisateur.
A réception du message chiffré, celui-ci utilisera sa clé privée pour le déchiffrer et sera ainsi le seul à pouvoir prendre connaissance du message.
L'avantage de cette solution est qu'il n'y a pas besoin d'échanger de clé de façon sécurisée car cette clé publique ne permet que le chiffrement et est donc à disposition de tout le monde.
Par MarcT0K (icônes par JGraph) CC BY-SA 4.0
Exemple du résultat de chiffrement du mot "Bonjour"avec l'algorithme RSA (Rivest Shamir Adleman) et une clé aléatoire de 4096 bits (on constate que le résultat est beaucoup plus volumineux qu'avec le chiffrement symétrique) :
-----BEGIN PGP MESSAGE-----
wcFMA0+nHCDs9qP5ARAAsrt0RSGo/8tLVp9xEgQVmrW7OgFgdXdMSs7B0NKITGOjPvBfYbkExFgL
S7KU6QkBQO1hdTKaP5n7GwJcIrhCvDL7pLXJfRFvqLcfYEkBjSWzz2Cyt/EZq0B/XtmxiWg8JJ+V
uKjSGBMRp1ksWAuFJvIyhDUOuvU2FEC1hC7jn5oSZr1Z4O2Kw8KtIR+ig8Ehscc3RzBH/GTRszLo
5xwFBdoz6cDGP98V/ezRTylZpoPfhaW91//DBtKBKWPnE+8rCdxXHyGIDxEkAG1DIvZoJtRh4HBZ
v5+5l+P5WjFo6BYU8uwx2WXbS0vUrMy8Z8bD9oME+c6Yy/8RLwABy/nn7T/ejpq6MgnP57P9LkoW
dD+8jrQgXQfXEhgWxON+QuXHBq5aoL/Avr9KNwNN7M+XNwXmgS4gkuHOevLNExSpnAnPAOIPKSf/
qEjm8yjFujLgt7wXOzosvHgVemwaK8OS0UnqAyoZL+6Y6uYK3VzzCG25+3TCVjcizjs1muQhvMgn
PK14UO6UYSgnisVx/Q7KYyciJYrfGxcfWDXGce6xJS6ktEUTLltuqEiJUSjktl7jbHEOpYF7Pxdf
sAzdsFNMZ65FHFYyIZ/Vg6glV4PaaH3QD4AWXMV+T6MM/cwzw+BhQvSbSjY12cHDf6mfQs5O2+sw
U/8/KaGEOMa1tcuNAdPSRAHfJeEDCyASipk1qW6ecY3UvKxBqxxauVdzu2LCiKmAzpKc1KkpNKyx
xpcHF+5IBPPNFHjFw6T6txuNH7UKc7+a1Rl8
=7arP
-----END PGP MESSAGE-----
L'inconvénient du chiffrement asymétrique :
- il faut pouvoir vérifier l'authenticité de la clé publique de l'interlocuteur.
- il est plus lent et gourmand en ressources que le chiffrement symétrique.
Fonctionnement.
Les algorithmes utilisent les propriétes mathématiques des nombres premiers (RSA), des courbes elliptiques sur des champs finis (ECC), ou des problèmes de logarithme discret (échange de clés Diffie-Hellman).
Ne rentrons pas dans le détail mais un petit rappel pour notre culture générale ne sera peut-être pas inutile... Au fait, c'est quoi déjà un nombre premier ? (c'est que c'est loin, la 5ème...): c'est un nombre entier qui possède uniquement 2 diviseurs positifs, 1 et lui-même.
1 n'est pas entier car il n'est divisible que par 1 (soit par 1 entier), 4 n'est pas entier car il est divisible par 2, 1 et lui-même (soit par 3 entiers), par contre 2 est entier car il n'est divisible que par 2 et 1.
Ces nombres premiers possèdent beaucoup de caractéristiques dont la plus simple est: tout nombre entier qui n'est pas premier est le produit d'au minimum 2 nombres premiers dont la décomposition est unique.
Les autres caractéristiques ne seront pas étudiées ici mais font appel aux notions de division euclidienne, indicatrice d'Euler, congruence, théorème de Bézout, Plus Grand Diviseur Commun, théorème de Fermat (bref, beaucoup de maths).
Retenons seulement que :
- La clé publique utilisée pour le chiffrement est générée à partir de la clé privée à l'aide d'une fonction mathématique.
- La réversibilité de cette fonction n'est pas impossible théoriquement.
- Sa résolution n'est toutefois pas à la portée des moyens techniques actuels lorsqu'il s'agit de factoriser de très grands nombres entiers en produit de nombres premiers.
Résoudre ce problème de réversibilité revient à casser le chiffrement, puisque si l'on arrive à calculer l'inverse de la fonction ayant produit cette clé publique, on obtient la clé privée et sommes donc en capacité de déchiffrer le message.
Sécurité des méthodes de chiffrement actuelles.
En préambule: tester toutes les combinaisons d'une clé numérique de 256 bits revient à tester 2256 soit 1.158x1077 possibilités. Cela prendrait des milliards d'années à un super-ordinateur capable de tester des milliards de clés par seconde.
- Les attaques par force brute sont donc aujourd'hui sans effet sur les algorithmes cryptographiques.
- Les autres attaques sur le chiffrement symétrique (hors l'attaque par clé apparentée mentionnée plus haut) ciblent plutôt l'implémentation matérielle plutot que l'algorithme lui-même (attaque par canal auxiliaire).
- La donne n'est par contre pas tout à fait la même pour la cryptographie à clé publique du fait de la méthode de calcul utilisée dans son algorithme de chiffrement car:
- En utilisant la méthode de calculs distribués (lorsque plusieurs ordinateurs travaillent ensemble), un nombre long de 795 bits a été factorisé.
- Les clés ont donc besoin d'être beaucoup plus grandes que pour les algorithmes de chiffrement symétrique pour un niveau de sécurité similaire (4096 contre 256 bits).
- Elle est vulnérable à l'algorithme quantique de Shor.
- Le plus grand danger auquel est confronté le chiffrement asymétrique à ce jour réside toutefois dans sa mise en oeuvre et se nomme attaque de l'homme du milieu (MITM ou Man In The Middle Attack):
- L'attaquant intercepte les clés publiques échangées et les remplace par la sienne.
- L'émetteur va donc chiffrer son message avec la clé publique de l'attaquant au lieu de celle du destinataire initial sans le savoir.
- L'attaquant pourra alors déchiffrer le message intercepté avec sa clé privée et le modifier. Puis il le rechiffrera avec la clé publique du destinataire avant de le lui renvoyer.
- Le destinataire déchiffrera le message reçu avec sa clé privée sans pouvoir se douter que celui-ci a été altéré par l'attaquant.
Chiffrement hybride.
Il résout les problématiques des chiffrements symétriques ou asymétriques utilisés seuls :
- On utilise le chiffrement asymétrique pour chiffrer une clé secrète avec la clé publique du destinataire puis on la lui transmet.
- On utilise le chiffrement symétrique pour chiffrer/déchiffrer avec la clé secrète ainsi sécurisée.
Cela règle le problème de distribution des clés et accélère la vitesse de chiffrement. Ces chiffrements sont par exemple mis en oeuvre pour sécuriser les communications internet (TLS), les connexions réseau (SSH), le chiffrement de certains emails (OpenPGP), etc...
Chiffrement post-quantique.
Bien que les algorithmes symétriques comme AES-256 soient considérés comme résistants aux attaques quantiques, il n'en est pas de même des algorithmes asymétriques.
C'est pour cette raison que certains fournisseurs de chiffrement ont déjà (ou sont en train) d'implémenter des algorithmes post-quantiques dans leurs applications.
La solution qu'ils retiennent consiste généralement à combiner des algorithmes de cryptographie traditionnels (comme AES et RSA) avec des algorithmes post-quantiques comme CRYSTALS-Kyber.
Rappelons que le NIST a retenu en 2022 un premier lot de quatre propositions d'algorithmes susceptibles de devenir les standards du chiffrement post-quantique: le chiffrement Kyber pour l’accès sécurisé aux sites web, les systèmes Sphinx+, Dilithium et Falcon pour les signatures numériques.
Intégrité des données : HACHAGE.
Objectif : S'assurer que les données qu'on reçoit ne sont pas altérées. Accessoirement, transformer la donnée en une autre beaucoup plus légère (moins gourmande en mémoire) et de taille fixe. Pour illustrer le principe, l'exemple de Wikipédia est très parlant :

Une fonction de hachage va transformer une donnée en une empreinte unique (aussi appelé condensat, hash, ou même haché). La fonction utilisée est telle qu'elle ne devra pas permettre de retrouver la donnée d'origine à partir de l'empreinte. L'objectif est uniquement de comparer des empreintes pour vérifier si elles sont identiques. Nous verrons dans la section sur les mots de passe que l'irréversibilité de la fonction de hachage est un élément clé du stockage des mots de passe sur serveur.
Risque : Utiliser un algorithme qui génère des "collisions", c'est à dire qui puisse générer une empreinte identique pour des données différentes. C'est le cas de l'algorithme MD5 (Message Digest), pourtant encore très (trop) présent pour protéger les mots de passe stockés sur les serveurs.
Authenticité des données : SIGNATURE NUMERIQUE.
Objectif : S'assurer de l'identité de l'auteur d'un document et de son intégrité.

Le chiffrement asymétrique est utilisé en inversant l'utilisation des clés par rapport au chiffrement. L'émetteur hache le message et le chiffre (signe) avec sa clé privée. Cela garantit son intégrité (hachage) et son identité (possession de la clé privée). Le destinataire le déchiffre avec la clé publique de l'émetteur.
La signature numérique a valeur légale (officiellement reconnue en Europe depuis janvier 2000), elle assure les mêmes garanties que la signature manuscrite, entre autre concernant sa fonction de non répudiation (l'impossibilité de nier avoir expédié le message). Il faut également noter que la signature n'est pas réutilisable, elle fait partie du document signé.
Risque : Utiliser un algorithme insuffisamment fort, problèmes liés à la diffusion de la clé publique et compromission de la clé privée.
Quelques exemples d'algorithmes :
| Type d'algorithme | Recommandé | Obsolescent |
|---|---|---|
| Chiffrement symétrique | [CHACHA20 / AES-256 /Twofish / Serpent] | [DES] |
| Chiffrement asymétrique | [RSA / Ed25519] | [RSASSA] |
| Chiffrement post-quantique | [Kyber / Sphinx+ / Dilithium / Falcon] | |
| Hachage | [SHA-256 / SHA-3] | [SHA-1] |
| Stockage mots de passe | [PBKDF2 / ARGON2 / Scrypt] | [MD5] |
Et vous, dans vos applis, quels sont les algorithmes utilisés ?
La technologie de chiffrement doit être utilisée lorsque vous surfez, communiquez, stockez des identifiants :
- Si le chiffrement est optionnel il doit être activé.
- S'il n'est pas proposé par votre application, elle doit être laissée de côté.
